【暴露】フィボナッチはインチキ、トレードで勝てない理由を解説

フィボナッチ数列とは

n番目のフィボナッチ数F_nの表し方（漸化式）
F₀=0，F₁=1　F(_n+2)=F(_n)+F(_n+1)　（n≧0）

F₂＝F₀+F₁=1（n=0）
F₃＝F₁+F₂=1+1＝2（n=1）
F₄＝F₂+F₃=1+2＝3（n=2）
F₅＝F₃+F₄=2+3＝5（n=3）
F₆＝F₄+F₅=3+5＝8（n=4）
F₇＝F₅+F₆=5+8＝13（n=5）

不思議なフィボナッチ数列

テクニカル分析の中に、「フィボナッチ」を使った分析手法があります。

これは、イタリアの数学者レオナルド・フィボナッチ氏が発見した数列で、フィボナッチ数列から導き出されるフィボナッチ比率、黄金比をトレードに役立てるというものです。

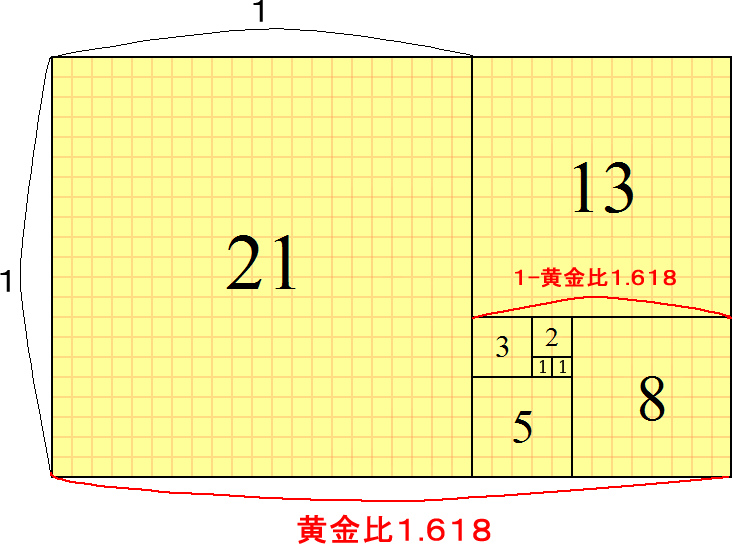
フィボナッチ数列は、「1、1、2、3、5,、8、 13、21、34、 55、89･･･」といった数列で、「連続した２項の和が次の項になる」という法則。「1+1＝2」、「1+2＝3」、「2+3＝5」、「3+5＝8」、「5+8＝13」という風に、前の２つの数値を足した数が並んでいくという規則性を持っています。

自然界に現れるフィボナッチ数列

この数列は自然界の中に見られ、ユリの花びらは3枚、桜や梅は5枚、コスモスは8枚、キク科植物は13枚、21枚、34枚、55枚など、この「フィボナッチ数列」に従って発生・成長しています。

その他、ひまわりの種の並びが螺旋状に21個、34個、55個、89個･･･となっていたり、葉の付き方や角度（葉序）、松ぼっくりのかさの並びやパイナップルの模様、身近なところではピアノの１オクターブが黒鍵5鍵、白鍵8鍵で合計13鍵になっていたり、様々なところにフィボナッチ数列が登場しています。

チャートにフィボナッチが出現!?

テクニカル分析としてのフィボナッチ

ところで、フィボナッチ数列の数字を、1つ前の数字で割ってみます。例えば、「3を2で割ると1.5」、「5を3で割ると1.67」、「8を5で割ると1.6」になります。このようにして数字を追いかけていくと、やがて黄金比である1.618に近づいていくことが分かります。

黄金比とは、二次方程式 x2− x − 1 = 0の正の解で、ギリシア文字の φ（ファイ）やτ（タウ）で表され、優れた芸術作品や建築物にこの比率が見られるほか、名刺や用紙サイズに利用されるなどバランスのとれた比率として知られています。

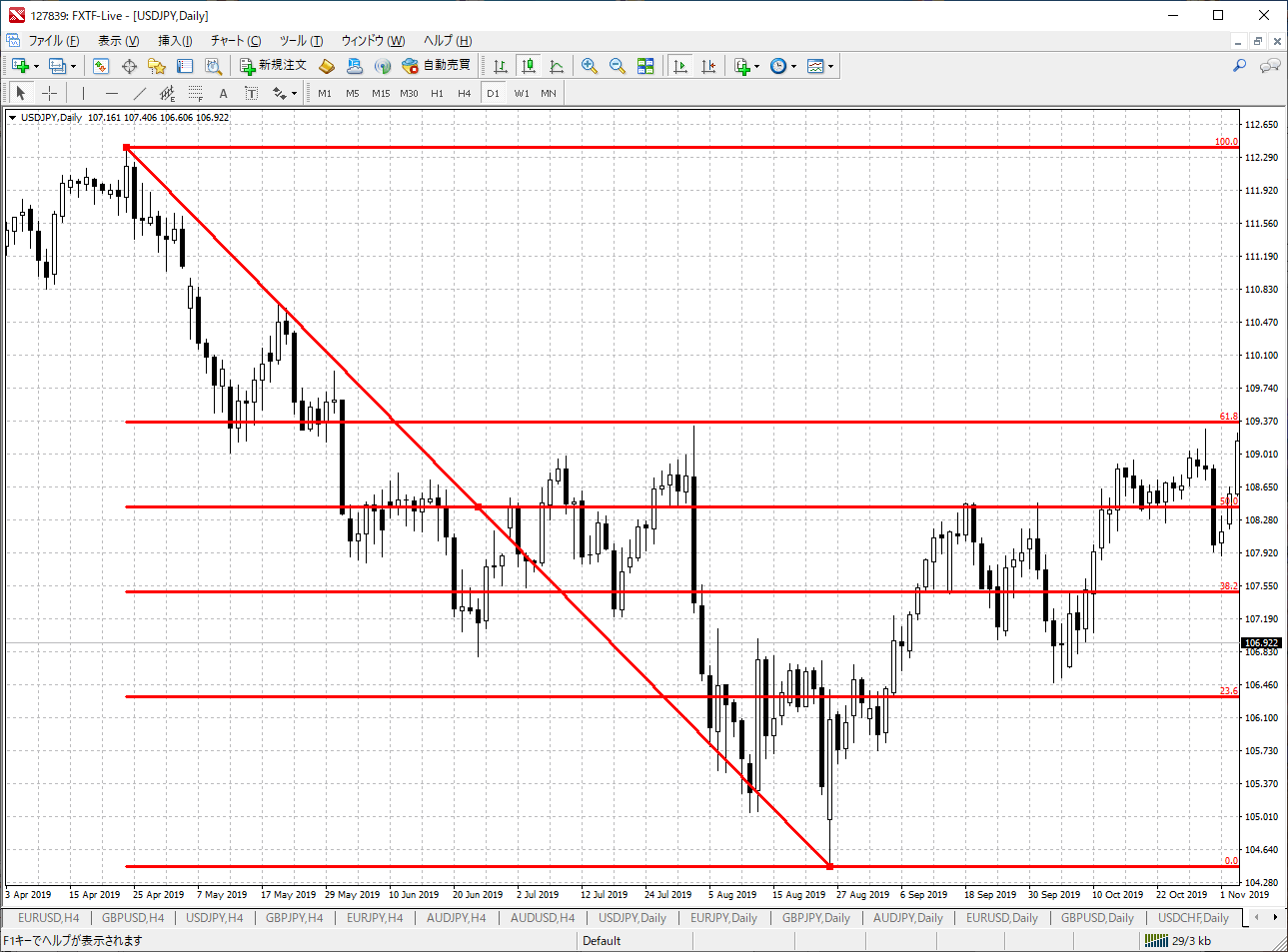
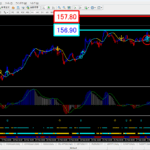
そして、この比率がＦＸや株のチャート上にサポートやレジスタンスラインとして発生、この分析を行う手法がフィボナッチになります。

具体的には、黄金比の0.618、0.618の平方根の0.786や1から0.618を引いた0.382がサポートやレジスタンスラインとして使われており、上記チャートのように的確に当てはまっていることが分かります。

フィボナッチと黄金比

黄金比を求める

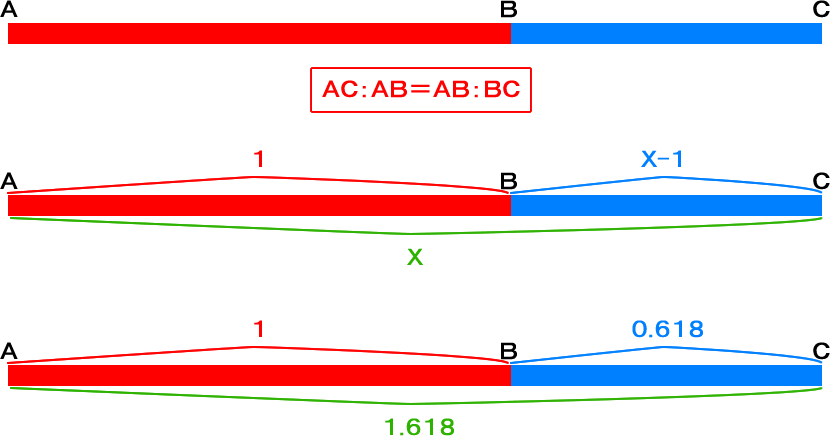
黄金比の図は、下記直線で表されます。

この時、黄金比を「X」とすると、「AC:AB＝AB:BC」より「X:1＝１：X-1」。これは、X²-X＝1、X²-X-1=0となり、この「X」の解が黄金比となります。

「X²-X-1=0」の解が黄金比

「X²-X-1=0」について、仮にＸを1にしてみると、1-1-1で解は-1となります。これでは0より小さくなってしまうので、Xは1より大きいことが分かります。次に、Xを2にしてみましょう。すると、4-2-1で1となり0より大きくなってしまうので、1より小さいことが分かります。

つまり、Xは1より大きくて2より小さい＝小数点の数というややこしい数値であることになります。そのため、この式でXについて解こうとした場合、最初の「X²」（Xの２乗）をなんとかする必要があります

そこで、この２乗を消すために、2次方程式を1次式の2乗の形に変形する平方完成を使います。

例えば、(X-1/2)²とすると、X²-x+1/4となってX²-xが出てきます。あとは、1/4が-1になればよいの-5/4足し、(X-1/2)²-5/4とします。

次に -5/4を右辺へ移動し、
(X-1/2)²＝5/4

(X-1/2)²の２乗を消すために両辺をルート化にします。

左辺は２乗部分が消え右辺がルート化するので、

X-1/2＝±√5/4

X＝1/2±(√5)/2
X=(1±√5)/2

√5は「2.2360679 （富士さんろくオウム鳴く）」
3.2360679÷2
1.61803395…

と、ここで黄金比の1.618が出てきます。

＜二次方程式 x²− x − 1 = 0 の解＞
x²-x-1=0

(x-1/2)²-1/4-1=0
(x-1/2)²-(5/4)=0（平方完成）
(x-1/2)²=(5/4)
x-(1/2)=±√(5/4)
x=(1/2)±√(5/4)
x=(1/2)±(√5)/2
x=(1±√5)/2
x=±1.618033988749895…

よく見るとそれほど合っていないフィボナッチ

フィボナッチ比率への疑問

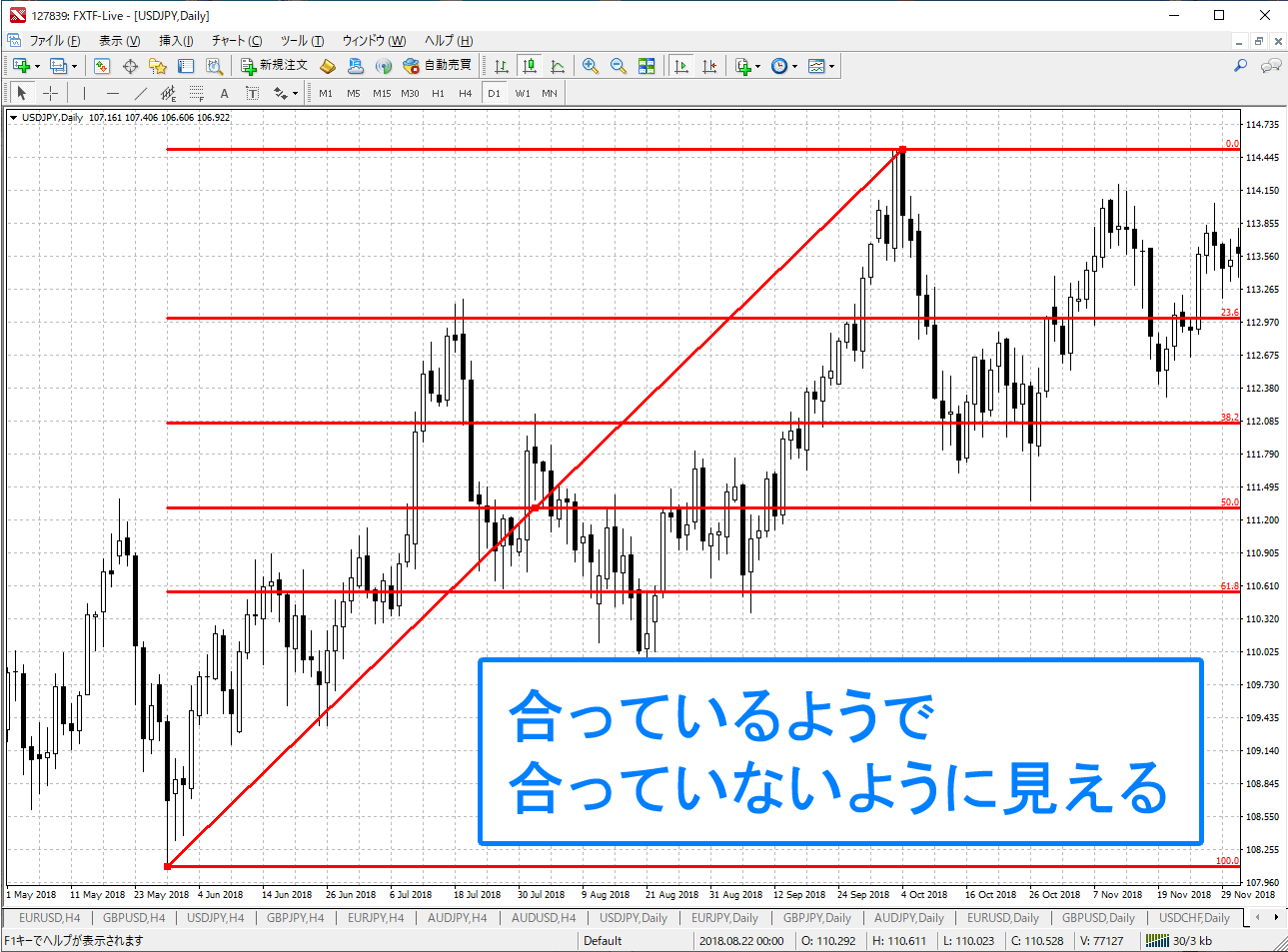
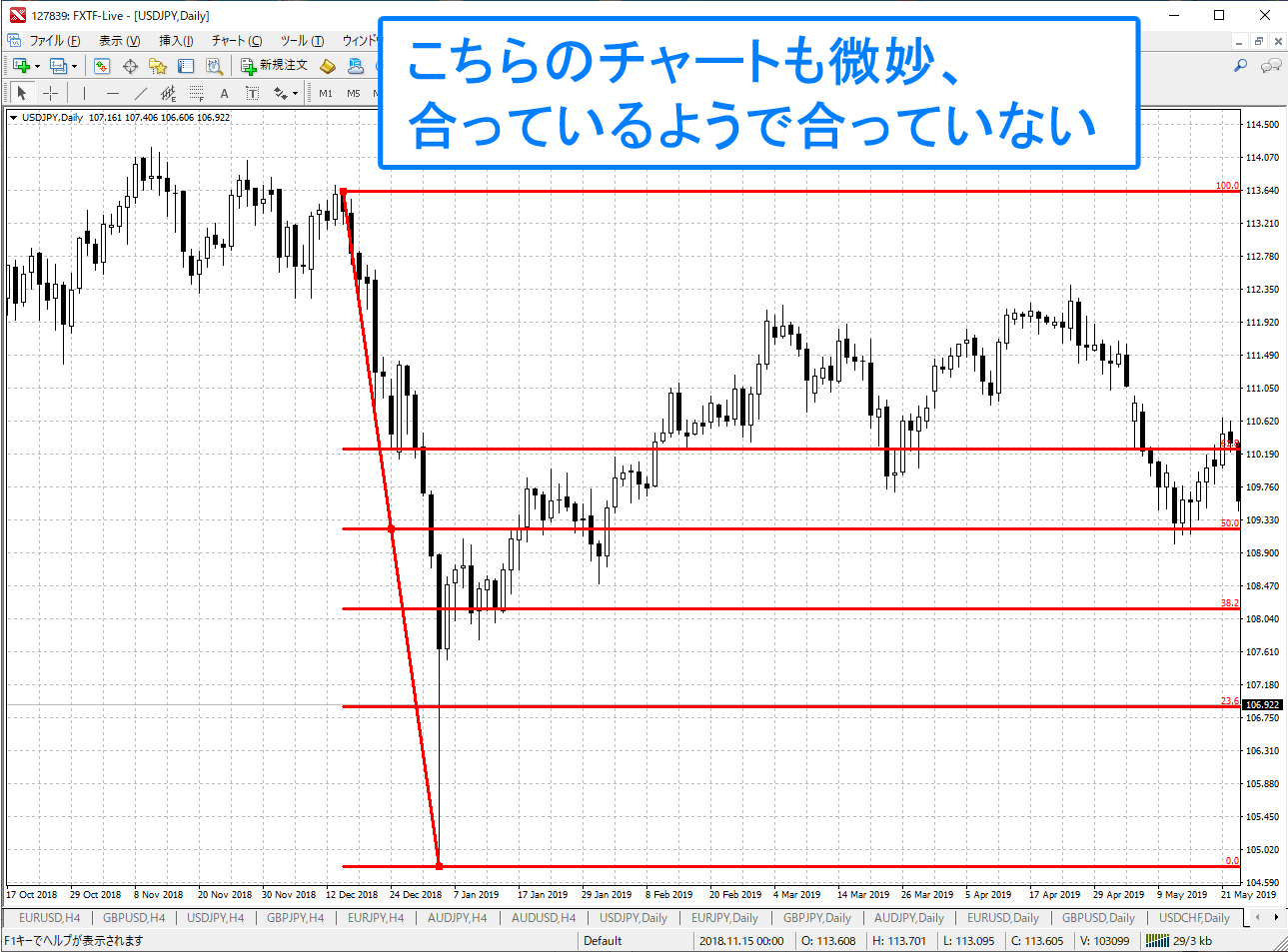
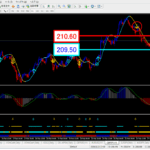
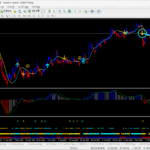
でも、ちょっと待ってください。実は先ほどのチャート、見つけるのに時間がかかっています。なぜなら、普通にフィボナッチを使うと、上のチャートのようにあまり意味のないチャートが出来上がるからです。

これらチャートのフィボナッチは一見するとサポート・レジスタンスラインになっているように見えますが、よく見るとそうでもないように見えます。つまり、ラインを引くことによって目の錯覚でどうとでも取れてしまうのです。これだと実際のトレードでは使えないです。

みなさんも、試しにチャートへフィボナッチを描画してみてください。他人に説明すると想定してチャートを探してみると、おそらくかなり時間がかかるとはずです。

また、どんなチャートでもラインを引くとサポート・レジスタンスラインっぽく見えてしまいます。ランダムな流れでもラインを引くと規則性が見えてきてしまうので、そのようなマジックに騙されないでください。

実は例外だらけで神秘性はない

【暴露】フィボナッチ数列になっていない花びら

何でもありで信頼性に欠ける

冒頭で、花びらの枚数がフィボナッチ数列に従っているという話をしましたが、実は例外がたくさんあります。アブラナの花びらは4枚、サフランは6枚だったり、7枚や11枚、18枚の花などの例外も多くあります。

ひまわりの螺旋も、花の大きさや種の詰まり具合で分岐したり途切れてしてしまうので、実際に数えてみるとフィボナッチ数列には従っていないことが分かります。だいたい、Wikipediaのフィボナッチ数列のページ真ん中にあるひまわりの螺旋が、フィボナッチ数列になっていないです。

要は、こじつけで何でも強引にフィボナッチになっています。

結論としては、フィボナッチ数列という数列自体はもちろん実在するのですが、それとマーケットの動きには関連性が見られない、ということになります。

メリットがあるとすれば、フィボナッチを見てトレードしたトレーダーが同じような注文をだすのでそういったところに注文が貯まりやすいということはあるかもしれませんが、それだとフィボナッチ数列の神秘性のかけらもなくなってしまうことになります。

フィボナッチ数列や黄金比は不思議なものでも何でもなく、都市伝説程度に見ておけばよいでしょう。

【暴露】Wikipediaのひまわり螺旋の数

【動画】フィボナッチ＆エリオット波動は嘘

【動画】FXのフィボナッチはインチキ